за обављање ова три поступка потребно је подсетити се дељења са остатком (целобројног дељења). Свако целобројно дељење може да се запише у облику a : b = k(r), r < b,, где је a дељеник, b делилац, k количник и r остатак. Остатак мора бити мање од делиоца јер у супротном дељење није коректно извршено.
Пример: Подели са остатком 134 и 9
У овом примеру смо добили количник 14 и остатак 8. То записујемо и овако:
134 : 9 = 14(8)
Код свих ових конверзија врши се дељење са остатком датог декадног броја основом система у који се пребацује, а затим се том основом дели добијени количник и тај поступак се понавља док се не добије количник 0. Приликом сваког овог корака памти се добијени остатак. Након тога се записују остаци почевши од последњег па до првог и добијени број је тражени декадни број. Представићемо ове поступке у следећим примерима.
Пребацивање из декадног у бинарни бројевни систем
Пребаци број 26(10) у бинарни бројевни систем
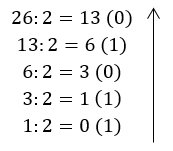
Пратећи стрелицу добијамо тражени број, тј. 26(10) = 11010(2)
Пребацивање из декадног у октални бројевни систем
Пребаци број 137(10) у октални бројевни систем
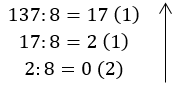
Решење је 137(10) = 211(8)
Пребацивање из декадног у хексадецимални бројевни систем
Код ове конверзије потребно је водити рачуна о томе да се остаци који су већи од 10 замене одговарајућим хексадецималним цифрама од A до F.
Пребаци број 949(10) у хексадецимални бројевни систем
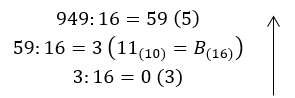
Решење је 949(10) = 3B5(16)